Correcting disagreements between noisy human-annotated data and predictions - Evaluation for Automated Evidence Synthesis

TLDR¶

Be careful when correcting disagreements between human and machine codes! We don’t fully understand how this works yet, but we can see it can cause issues Skip to summary

How to deal with imperfections in gold-standard data¶

In order to evaluate AI classifiers, we compare the output of a classifier to ground truth data. Usually, this ground-truth is generated by humans.

In practice, we know that humans err when classifying texts, and that even gold-standard data, which is checked by multiple expert humans, can err too.

Here we think through some issues on how to deal with this imperfection

Ground truth data¶

Let’s start by creating some real ground truth data. These represent the absolutely true values, if we can suspend our disbelief that such a thing is epistemically possible.

import numpy as np
import numpy.typing as npt
from sklearn.metrics import cohen_kappa_score, recall_score, precision_score

N = 100
prevalence = 0.2
included = round(N*prevalence)
np.random.seed(5)
values = np.concatenate([
    np.ones(included),
    np.zeros(N-included)
])
y_true = np.random.choice(values, values.shape[0])
y_true

array([0., 0., 0., 1., 0., 1., 0., 0., 0., 0., 1., 0., 1., 0., 0., 0., 0.,
       0., 0., 0., 0., 0., 0., 0., 1., 1., 0., 0., 1., 0., 1., 0., 1., 0.,
       1., 0., 1., 0., 0., 0., 0., 1., 0., 0., 0., 1., 1., 1., 0., 0., 1.,
       0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1., 0., 1., 0., 0.,
       1., 0., 0., 1., 1., 0., 0., 0., 0., 1., 0., 0., 0., 0., 1., 1., 0.,
       0., 0., 1., 1., 0., 1., 0., 1., 0., 0., 0., 0., 0., 1., 0.])

Imperfect human data¶

Now let’s imagine that we have a human coder who has a set probability of correctly identifying 1s in the ground truth data, and a set probability of correctly identifying 0s. To stop ourselves rewriting code as we add more coders, we will write a class to handle the common things we want to do with coders.

human_coding_ability = 0.8

class Metrics():
    pass

class Coder():

    def __init__(self):
        self.val_metrics = {}

    def code(self, y_true: npt.NDArray, prob_1: float, prob_0: float):
        odds = y_true.copy()
        odds[odds==1] = prob_1
        odds[odds==0] = prob_0
        self.codes = np.random.binomial(1, odds)

    def evaluate(self, y_true: npt.NDArray, truth_label: str):
        self.val_metrics[truth_label] = Metrics()
        self.val_metrics[truth_label].recall = recall_score(y_true, self.codes)
        self.val_metrics[truth_label].precision = precision_score(y_true, self.codes)
        self.val_metrics[truth_label].cohen_kappa = cohen_kappa_score(y_true, self.codes)
        self.val_metrics[truth_label].irr = (y_true==self.codes).sum() / y_true.shape[0]
        
human_1 = Coder()

human_1.code(
    y_true=y_true, 
    prob_1=human_coding_ability, 
    prob_0=1-human_coding_ability
)

human_1.codes

array([0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0,
       0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0,
       1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1,
       0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0,
       1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0])

We can now quantify their performance.

human_1.evaluate(y_true, "ground_truth")

In this case, the human’s recall score is 0.74, and their precision score is 0.59

We have correctly built an imperfect human.

Now let’s add two more humans. The first also classifies each document, and the second classifies each document that the first two disagree on. Each human has the same ability to code. That is, they have an 80% chance of coding both 1s and 0s correctly.

We’ll start by adding the second human and looking at inter-rater reliability scores

human_2 = Coder()

human_2.code(
    y_true = y_true,
    prob_1=human_coding_ability, 
    prob_0=1-human_coding_ability
)

human_1.evaluate(human_2.codes, "human_2")
human_2.evaluate(y_true, "ground_truth")

According to a simple measure of agreement, the two coders agree on 67% of records. Adjusting for how likely this could happen by chance, their Cohen’s Kappa score is 0.32

Gold standard data¶

Now we’ll generate codes for human 3, which we can use whenever humans 1 and 2 disagreed.

human_3 = Coder()

human_3.code(
    y_true = y_true,
    prob_1=human_coding_ability, 
    prob_0=1-human_coding_ability
)
human_3.evaluate(y_true, "ground_truth")

disagreements = np.argwhere(human_1.codes!=human_2.codes).ravel()

And generate our gold standard data.

gold_standard = Coder()

gold_standard.codes = human_1.codes.copy()
gold_standard.codes[disagreements] = human_3.codes[disagreements]

gold_standard.evaluate(y_true, "ground_truth")

Our gold standard data now has a recall score of 0.87, and a precision score of 0.77

import matplotlib.pyplot as plt

fig, ax = plt.subplots()

coders = [human_1, human_2, human_3, gold_standard]

ax.barh(
    range(len(coders)),
    [x.val_metrics["ground_truth"].recall for x in coders],
)

ax.set_yticks(range(len(coders)))
ax.set_yticklabels(["Human 1", "Human 2", "Human 3", "Gold standard"])
plt.show()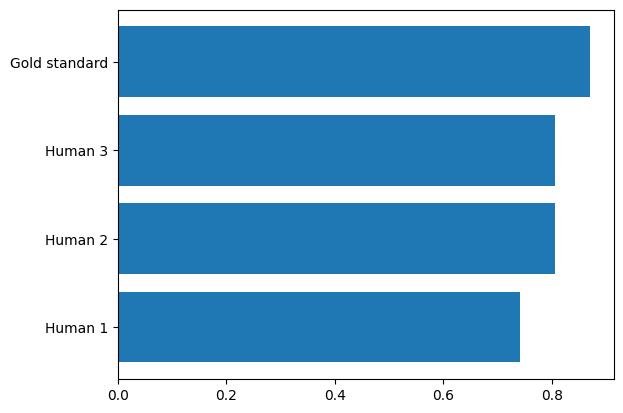

We can see that by combining labels across humans, we can create data of higher quality than the average human coder.

AI predictions¶

Better than human performance¶

Now let’s generate some predictions that might have come from an LLM. Let’s assume that LLMs achieve “better-than-human performance” (by 5%) and increase the chances of correctly identifying 1s and 0s by a few percentage points.

llm_superior = Coder()

llm_superior.code(
    y_true,
    human_coding_ability*1.05,
    1-human_coding_ability*1.05
)

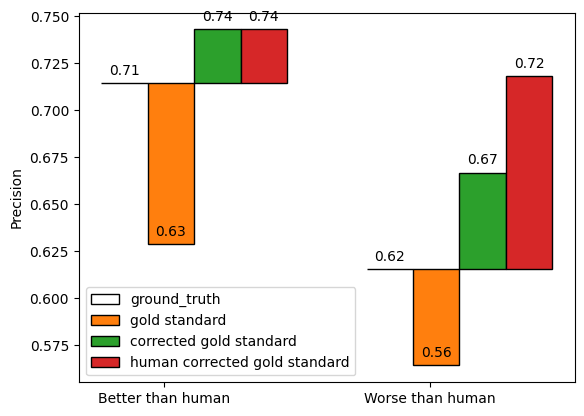
llm_superior.evaluate(y_true, "ground_truth")

Our llm achieves a recall score of 0.81, and a precision score of 0.81.

Comparing to imperfect gold-standard data¶

Now let’s see what happens when use gold standard data (instead of the epistemically questionable true ground truth data)

llm_superior.evaluate(gold_standard.codes, "gold standard")

Using our gold standard data, we measure our llm as achieving a recall score of 0.63, and a precision score of 0.63.

Correcting gold-standard data with the truth¶

First, let us imagine that, when we look into the cases where the gold standard data and the llm disagree, we can reveal the “true” value of the ground truth, and correct the gold-standard data accordingly.

gold_llm_disagreements = np.argwhere(gold_standard.codes!=llm_superior.codes)
gold_corrected = gold_standard.codes.copy()
gold_corrected[gold_llm_disagreements] = y_true[gold_llm_disagreements]

llm_superior.evaluate(gold_corrected, "corrected gold standard")

Using the corrected gold standard data, we now measure our llm as achieving a recall score of 0.81, and a precision score of 0.74.

Correcting gold-standard data with human-codes¶

This is probably a strange assumption, since we can only “correct” errors co-inciding with disagreements by getting a 4th human to look at the record again, but as we saw before, humans are sadly imperfect coders.

human_4 = Coder()

human_4.code(
    y_true = y_true,
    prob_1=human_coding_ability, 
    prob_0=1-human_coding_ability
)

gold_corrected_human = gold_standard.codes.copy()

gold_corrected_human[gold_llm_disagreements] = human_4.codes[gold_llm_disagreements]

llm_superior.evaluate(gold_corrected, "human corrected gold standard")

In this case, using the human-corrected gold standard data, we now measure our llm as achieving a recall score of 0.81, and a precision score of 0.74.

Worse than human performance¶

Now let’s assume that LLMs perform worse than humans. Perhaps we did not engineer our prompts very well, and forgot to tell the LLM to be a very good coder.

llm_inferior = Coder()

llm_inferior.code(
    y_true,
    human_coding_ability*0.95,
    1-human_coding_ability*0.95
)

llm_inferior.evaluate(y_true, "ground_truth")

Our llm achieves a recall score of 0.77, and a precision score of 0.77.

Comparing to imperfect gold-standard data¶

Now let’s see what happens when use gold standard data (instead of the epistemically questionable true ground truth data)

llm_inferior.evaluate(gold_standard.codes, "gold standard")

Using our gold standard data, we measure our llm as achieving a recall score of 0.63, and a precision score of 0.63.

Correcting gold-standard data with the truth¶

gold_llm_disagreements = np.argwhere(gold_standard.codes!=llm_inferior.codes)
gold_corrected = gold_standard.codes.copy()
gold_corrected[gold_llm_disagreements] = y_true[gold_llm_disagreements]

llm_inferior.evaluate(gold_corrected, "corrected gold standard")

Using the corrected gold standard data, we now measure our llm as achieving a recall score of 0.79, and a precision score of 0.79.

Correcting gold-standard data with human-codes¶

This is probably a strange assumption, since we can only “correct” errors co-inciding with disagreements by getting a human to look at the record again, but as we saw before, humans are sadly imperfect coders.

gold_corrected_human = gold_standard.codes.copy()

gold_corrected_human[gold_llm_disagreements] = human_4.codes[gold_llm_disagreements]

llm_inferior.evaluate(gold_corrected_human, "human corrected gold standard")

In this case, using the human-corrected gold standard data, we now measure our llm as achieving a recall score of 0.8, and a precision score of 0.8.

Summary¶

Now we can compare the recall we would observe LLMs better and worse than human using different idealised, uncorrected, or corrected evaluation datasets.

We can see that comparing AI labellers to human labellers results in an overly pessimistic estimate of their true performance (as compared to the ground truth data). However, correcting disagreements results in an overly optimistic estimate of their true performance. This is because we “catch” human errors where they incorrectly disagreed with AI predictions, but do not catch AI errors when both the human and the prediction erred. Pessimism is greater, and optimism is lesser, where the AI produces fewer errors than humans.

import matplotlib.pyplot as plt

fig, ax = plt.subplots()

def hat_graph(ax, xlabels, values, group_labels):
    """
    Create a hat graph.

    Parameters
    ----------
    ax : matplotlib.axes.Axes
        The Axes to plot into.
    xlabels : list of str
        The category names to be displayed on the x-axis.
    values : (M, N) array-like
        The data values.
        Rows are the groups (len(group_labels) == M).
        Columns are the categories (len(xlabels) == N).
    group_labels : list of str
        The group labels displayed in the legend.
    """

    def label_bars(heights, rects):
        """Attach a text label on top of each bar."""
        for height, rect in zip(heights, rects):
            ax.annotate(f'{height:.2}',
                        xy=(rect.get_x() + rect.get_width() / 2, height),
                        xytext=(0, 4),  # 4 points vertical offset.
                        textcoords='offset points',
                        ha='center', va='bottom')

    values = np.asarray(values)
    x = np.arange(values.shape[1])
    ax.set_xticks(x, labels=xlabels)
    spacing = 0.3  # spacing between hat groups
    width = (1 - spacing) / values.shape[0]
    heights0 = values[0]
    for i, (heights, group_label) in enumerate(zip(values, group_labels)):
        style = {'fill': False} if i == 0 else {'edgecolor': 'black'}
        rects = ax.bar(x - spacing/2 + i * width, heights - heights0,
                       width, bottom=heights0, label=group_label, **style)
        label_bars(heights, rects)

comparisons = [
    "ground_truth",
    "gold standard",
    "corrected gold standard",
    "human corrected gold standard"
]
coders = [llm_superior, llm_inferior]

vals = np.array([
    [x.val_metrics[y].recall for y in comparisons]
    for x in coders
]).T

hat_graph(ax, ["Better than human","Worse than human"], vals, comparisons)

ax.set_ylabel("Recall")

ax.legend()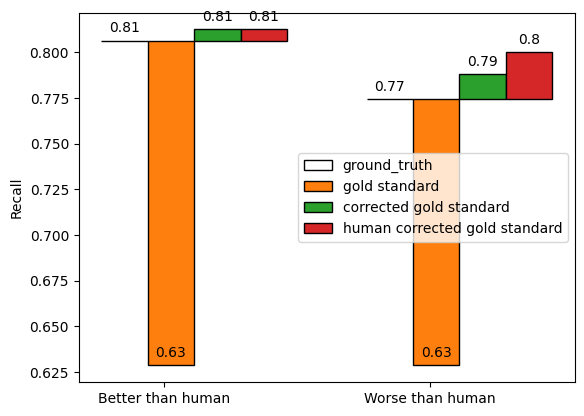

fig, ax = plt.subplots()

vals = np.array([
    [x.val_metrics[y].precision for y in comparisons]
    for x in coders
]).T

hat_graph(ax, ["Better than human","Worse than human"], vals, comparisons)

ax.set_ylabel("Precision")

ax.legend()